(Q5). A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of
1
4
 m and a tread of
1
2
 m. (see Fig.). Calculate the total volume of concrete required to build the terrace.

[Hint: Volume of concrete required to build the first step =
1
4
 ×
1
2
 × 50 m]

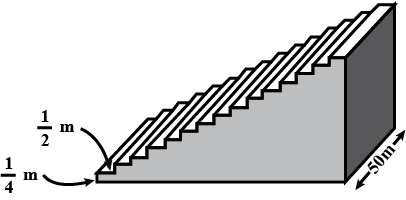
Length of each step = 50 m = l

Rise/height of each step =
1
4
 m = h
Tread of each step =
1
2
 m = b
Given volume of concrete required to build the first step =
1
4
 ×
1
2
 × 50 m3 = lbh

We can compare the shape of each step with a cuboid.

Volume of the cuboid = . .

Volumes of concrete required to build the 15 steps are

{ 50 ×
1
4
 ×
1
2
 } + { 50 × ( ×
1
4
 ) ×
1
2
 } + { 50 × ( ×
1
4
 ) ×
1
2
 } + ........ + { 50 × ( ×
1
4
 ) ×
1
2
 } m3
= [
50
 × +
50
 × +
50
 × + ........ +
50
 × ] m3
=
50
 [ + + + ........ + ]

[∵ 1, 2, 3,.... 15 is in A.P. where a = ; d = , n = ]

Sn =
n
2
 [2a + (n - 1)d]
=
50
 ×
2
 [ 2 × + ( - 1) × ]
=
50
 ×
2
 × [ + ] m3
=
50
 ×
2
 × = [ × ] = m3

∴ The total volume of concrete required to build the terrace is m3.