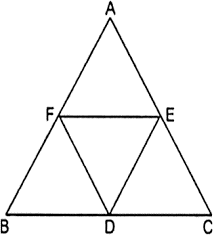
(Q4) D, E, F are midpoints of sides BC, CA, AB of ∆ABC. Find the ratio of areas of ∆DEF and ∆ABC.

Solution :

Given in ∆ABC D, E, F are the midpoints of the sides BC, CA and AB.

In ∆ABC, EF is the line join of mid-points of two sides AB and AC of ∆ABC.

Thus ∥ [∵
AF
FB
 =
AE
EC
 Converse of B.P.T.]

Similarly DE divides AC and BC in the same ratio, i.e., DE ∥ .

Now in □ BDEF, both pairs of opposite sides (BD ∥ EF and DE ∥ BF) are parallel.

Hence □ BDEF is a where is a diagonal.

∴ ∆ ≃ ∆ .....(1)

Similarly we can prove that

∆DEF ≃ ∆ .....(2)

[∵ CDFE is a parallelogram]

∆DEF ≃ ∆ .....(3)

[∵ □ AEDF is a parallelogram]

From (1), (2) and (3)

∆ ≃ ∆DEF ≃ ∆ ≃ ∆CDE

Also, ∆ABC = ∆ + ∆DEF + ∆ + ∆CDE = .∆

Hence, ∆ABC : ∆DEF = : .